Table Of Content

The data are shown in Figure 7.1B, where we connect the three observed enzyme levels in each block by a line, akin to an interaction plot. The vertical dispersion of the lines indicates that enzyme levels within each litter are systematically different from those in other litters. The lines are roughly parallel, which shows that all three drug treatments are affected equally by these systematic differences, there is no litter-by-drug interaction, and treatment contrasts are unaffected by systematic differences between litters.
Block Randomization
Here is a plot of the least squares means for Yield with all of the observations included. Where F stands for “Full” and R stands for “Reduced.” The numerator and denominator degrees of freedom for the F statistic is \(df_R - df_F\) and \(df_F\) , respectively. Below is the Minitab output which treats both batch and treatment the same and tests the hypothesis of no effect. Imagine an extreme scenario where all of the athletes that are running on turf fields get allocated into one group and all of the athletes that are running on grass fields are allocated into the other group. In this case it would be near impossible to separate the impact that the type of cleats has on the run times from the impact that the type of field has. Suppose engineers at a semiconductor manufacturing facility want to test whether different wafer implant material dosages have a significant effect on resistivity measurements after a diffusion process taking place in a furnace.
Table of Contents
Because of the restricted layout, one observation per treatment in each row and column, the model is orthogonal. This property has an impact on how we calculate means and sums of squares, and for this reason, we can not use the balanced ANOVA command in Minitab even though it looks perfectly balanced. We will see later that although it has the property of orthogonality, you still cannot use the balanced ANOVA command in Minitab because it is not complete. When the data are complete this analysis from GLM is correct and equivalent to the results from the two-way command in Minitab. It would reduce the overall effect of that treatment, and the estimated treatment mean would be biased. Before high-speed computing, data imputation was often done because the ANOVA computations are more readily done using a balanced design.
4.3 Crossing Blocks: Latin Squares
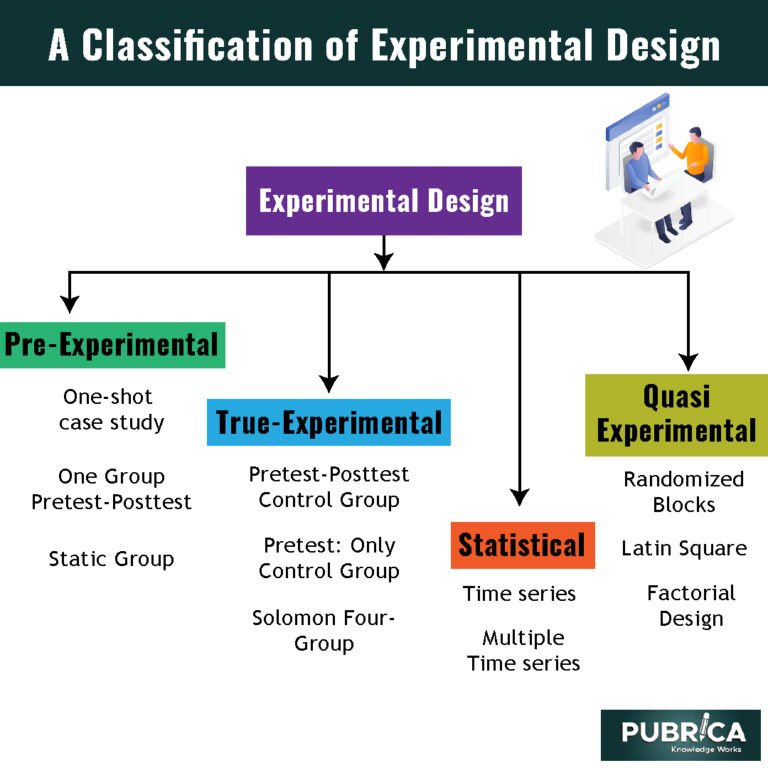
Each treatment occurs exactly once per row and once per column and the latin square design imposes two simultaneous constraints on the randomization of drugs on mice. A simple yet powerful design is the randomized complete block design (RCBD), where each block has as many units as there are treatments, and we randomly assign each treatment to one unit in each block. We can extend it to a generalized randomized complete block design (GRCBD) by using more than one replicate of each treatment per block. If the block size is smaller than the number of treatments, a balanced incomplete block design (BIBD) still allows treatment allocations balanced over blocks such that all pair contrasts are estimated with the same precision.
This Lego experiment shows our brains prefer adding. Here's why it matters - World Economic Forum
This Lego experiment shows our brains prefer adding. Here's why it matters.
Posted: Wed, 21 Apr 2021 07:00:00 GMT [source]
Statistical Analysis of the Latin Square Design
Here is an alternative way to analyze this design using the analysis portion of the fractional factorial software in Minitab v.16. Using an experiment-wise error rate of 5%, we see significant differences between materials A and B, A and C, A and D, and B and C. We can study the data graphically, plotting by treatment and by block. Minitab’s General Linear Command handles random factors appropriately as long as you are careful to select which factors are fixed and which are random.
In the first RCBD (Figure 7.3B), we create a blocking factor ‘above’ the original experimental unit factor and group mice by their litters. In the second RCBD (Figure 7.3C), we subdivide the experimental unit into smaller units by taking multiple samples per mouse. This re-purposes the original experimental unit factor as the blocking factor and introduces a new factor ‘below,’ but requires that we now randomize Drug on (Sample) to obtain an RCBD and not pseudo-replication. In an ideal situation, a completely randomized full factorial with multiple numerous replications would make a lot of statistical theoretical sense, including reducing the confidence interval, the higher power of the findings, and so on. In fact, completely randomized design has been considered the most efficient over the years.
In some scenarios, however, it is necessary to use more than one replicate of each treatment per block. This is typically the case if our blocking factor is non-specific and introduced to capture grouping due to the logistics of the experiment. For example, we might conduct our drug comparisons in two different laboratories.
Note that blocking is a special way to design an experiment, or a special“flavor” of randomization. Blocking can also be understood as replicating an experimenton multiple sets, e.g., different locations, of homogeneous experimental units,e.g., plots of land at an individual location. The experimental units shouldbe as similar as possible within the same block, but can be very differentbetween different blocks.
This type of design can be extended to an arbitrary number of nested blocks and we might use two labs, two cages per lab, and two litters per cage for our example. As long as each nested factor is replicated, we are able to estimate corresponding variance components. If a factor is not replicated (e.g., we use a single litter per lab), then there are no degrees of freedom for the nested blocking factor, and the effects of both blocking factors are completely confounded.
The definition and analysis of linear contrasts work exactly as for the two-way ANOVA in Section 6.6, and contrasts are defined on the six treatment group means. For direct comparison with our previous results, we estimate the two interaction contrasts of Table 6.6 in the blocked design. They compare the difference in enzyme levels for D1 (resp. D2) under low and high fat diet to the corresponding difference in the placebo group; estimates and Bonferroni-corrected confidence intervals are shown in Table 7.2. Properties non-specific to the experimental units include (i) batches of chemicals used for the experimental unit; (ii) device used for measurements; or (iii) date in multi-day experiments. These are often necessary to account for systematic differences from the logistics of the experiment (such as batch effects); they also increase the generalizability of inferences due to the broader experimental conditions. The omnibus \(F\)-test for the treatment factor provides clear evidence that the drugs affect the enzyme levels differently and the differences in average enzyme levels between drugs is about 85 times larger than the residual variance.
Identify potential factors that are not the primary focus of the study but could introduce variability. In this design, you would have exactly two of each type of dough in each of the oven runs. Connect and share knowledge within a single location that is structured and easy to search. That is, the presence or absence of the block parameters does not affect the estimator of the treatment parameters (and vice versa). We can create a (random) Latin Square design in R for example with thefunction design.lsd of the package agricolae (de Mendiburu 2020). And the 12 machines are distinguished by nesting the i index within the h replicates.
Special considerations for labeled experiments,experiments with reference samples, and experiments with repeatedmeasures are provided at the end. This paper develops the idea of min–max robust experiment design for dynamic system identification. The idea of min–max experiment design has been explored in the statistics literature. However, the technique is virtually unknown by the engineering community and, accordingly, there has been little prior work on examining its properties when applied to dynamic system identification. The paper considers linear systems with energy (or power) bounded inputs.
All you have to do is go through your blocks one by one and randomly assign observations from each block to treatment groups in a way such that each treatment group gets a similar number of observations from each block. You can see this by these contrasts - the comparison between block 1 and Block 2 is the same comparison as the AB contrast. Note that the A effect and the B effect are orthogonal to the AB effect. This design gives you complete information on the A and the B main effects, but it totally confounds the AB interaction effect with the block effect. The reference design or design for differential precision is a variation of the BIBD that is useful when a main objective is comparing treatments to a control (or reference) group.
The measurement at this point is a direct reflection of treatment B but may also have some influence from the previous treatment, treatment A. This is a Case 2 where the column factor, the cows are nested within the square, but the row factor, period, is the same across squares. The simplest case is where you only have 2 treatments and you want to give each subject both treatments.
Let’s take participant gender in a simple 3-factor experiment as an example. We use the usual aov function with a model including the two main effectsblock and variety. It is good practice to write the block factor first; incase of unbalanced data, we would get the effect of variety adjusted for blockin the sequential type I output of summary, see Section 4.2.5and also Chapter 8. Note that the least squares means for treatments when using PROC Mixed, correspond to the combined intra- and inter-block estimates of the treatment effects.
We assume that the parameters lie in a given compact set and optimise the worst case over this set. We also provide a detailed analysis of the solution for an illustrative one parameter example and propose a convex optimisation algorithm that can be applied more generally to a discretised approximation to the design problem. We also examine the role played by different design criteria and present a simulation example illustrating the merits of the proposed approach.
No comments:
Post a Comment